Correction Exercice N°5 - Bioénergétique oxydo-réduction : chaîne respiratoire -force proton motrice - synthèse d'ATP
Voir l'énoncé.

 

 

Fonctionnement de la chaîne respiratoire :

 

  • transfert des électrons
  • consommation d'oxygène (complexe IV)
  • expulsion des protons vers l'espace intermembranaire (force proton motrice)
  • synthèse d'ATP avec retour de 3 protons vers la matrice (dissipation du gradient)

metabolisme chaine respiratoire gradient electrochimique force proton motrice oxydo reduction ATP synthase biochimej

Schéma général de la chaîne respiratoire

metabolisme chaine respiratoire gradient electrochimique force proton motrice oxydo reduction ATP synthase biochimej

Source : KEGG

Retour haut de page

a. Calcul de la variation de l'énergie libre de Gibbs standard de la réoxydation du NADH

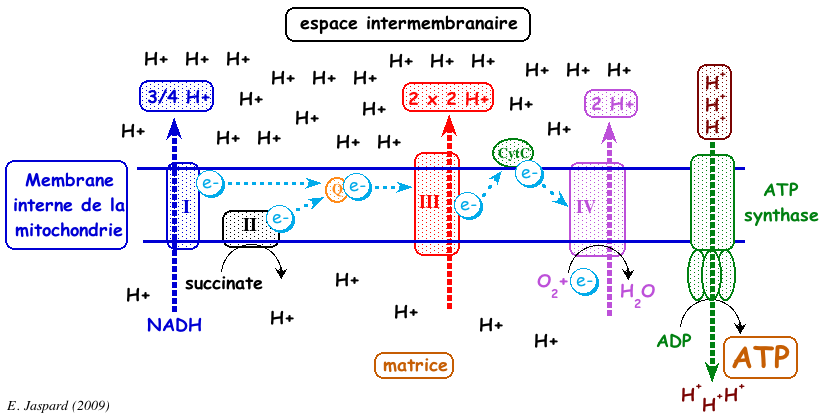
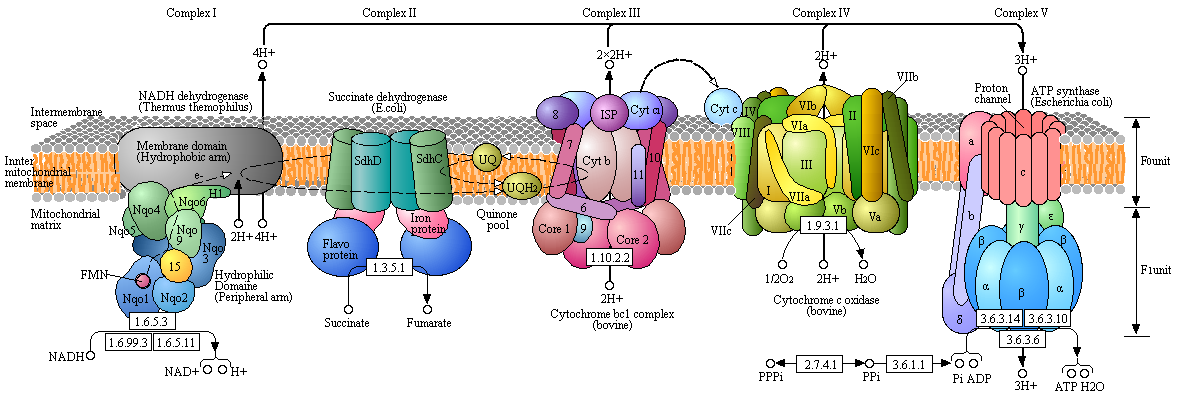
Les deux-demi réactions rédox sont :

  •                NADH + H+ <=> NAD+ + 2 H+ + 2 e-
  • 1/2 O2 + 2 H+ + 2 e- <=> H2O

Réaction globale : NADH + H+ + 1/2 O2 <=> NAD+ + H2O

Avec : E°'(NAD+/NADH) = - 0,32 V et E°'(O2/H2O) = + 0,82 V

Différence de potentiel rédox standard : ΔE°' = E°'(O2/H2O) - E°'(NAD+/NADH) = 0,82 - (- 0,32) = + 1,14 V

Donc : ΔG°'(réoxydation NADH) = - n . F . ΔE°' = - 2 x 96500 x 1,14 = - 216 kJ.mol-1

Voir un cours sur la variation d'énergie libre de Gibbs dans les conditions standard. 

Retour haut de page

b. Calcul de la variation d'énergie libre de Gibbs associée à l'expulsion d'un proton

La variation d'énergie libre du transfert de protons s'écrit : ΔG'(H+) = RT Ln ([H+]ext / [H+]int) + (zH+ . F . ΔΨ)

Par ailleurs : pH = - log([H+]) et Ln(a) = 2,3 . log10a => ΔG'(H+) = 2,3 . RT (pHint- pHext) + (zH+ . F . ΔΨ)

Où :

  • (pHint- pHext) = - (- 1,4) = 1,4 unités pH
  • zH+ = +1
  • ΔΨ = 140 mV = 0,14 V

Donc : ΔG'(H+) = (2,3 x 8,31 x 310 x 1,4) + (1 x 96500 x 0,14) = + 21,8 kJ.(mol H+ expulsé)-1

Retour haut de page

c. Nombre maximum théorique de protons expulsés lors de la réoxydation d'une mole de NADH,H+

Ce nombre théorique est donné par le rapport : nH+  =  |ΔG°'(réoxydation)| / |ΔG'(H+)| = - 216 kJ.mol-1 / + 21,8 kJ.(mol H+ expulsé)-1

Soit environ 10 protons expulsés.(mol NADH réoxydé)-1.

Retour haut de page

d. Nombre minimal de protons qui doivent rentrer pour permettre la synthèse d'une mole d'ATP.

La réaction de synthèse de l'ATP s'écrit : ADP + Pi  <=>  ATP + H2O

K'φ est la constante définie par le rapport des concentrations physiologiques des métabolites : K'φ = [ATP]φ / ([ADP]φ . [Pi]φ)

La concentration de l'eau (# 55,5 M) est considérée comme une constante.

Comme [ATP]φ = [ADP]φ = [Pi]φ = 10-2 M, alors K'φ = 102 M-1.

Donc : ΔG'(synthèse ATP) =  ΔG°'(synthèse ATP) + RT . Ln (K'φ) = (30,6) + (8,31 x 310 x Ln 102) = + 42 kJ.mol-1

Le nombre minimal de protons qui doivent rentrer est donc : mH+ =  |ΔG'(synthèse ATP)| / |ΔG'(H+)| = 2 protons

  • Cependant, 3 protons sont nécessaires à l'ATP synthase pour synthétiser une molécules d'ATP du fait du mécanisme structural et fonctionnel de l'ATP synthase.

Voir un cours sur la synthèse d'ATP.

Retour haut de page