
| Notions de base de mécanique moléculaire et de modélisation moléculaire des protéines |
| Tweet |
 |
|
1. Principe de la mécanique moléculaire
2. Le champ de force associé aux atomes d'une protéine
3. Modélisation de structures de protéines par homologie
|
4. Les scores de distances inter-atomiques entre des structures comparées 5. Exemples de programmes de modélisation et de visualisation de structures de protéines
6. "Protein threading" 7. Démarche "de novo protein design" : exemple de la protéine artificielle TOP7 8. Méthode Rosetta 9. Liens Internet et références bibliographiques |
|
1. Principe de la mécanique moléculaire La mécanique moléculaire a pour but de prédire l'énergie associée à une conformation donnée d'une molécule. Le résultat obtenu est comparé aux propriétés physiques de la molécule observées expérimentalement (structure tri-dimensionnelle déterminée par une méthode physique). C'est une méthode empirique qui utilise un modèle mathématique et divers paramètres de potentiels : l'ensemble [modèle mathématique / paramètres de potentiels] s'appelle un champ de force ("force field"). Les protéines sont constitués de centaines ou de milliers d'atomes et les seules méthodes de calculs pour des systèmes de cette taille sont les calculs de mécanique moléculaire. La mécanique quantique permet d'étudier des systèmes ne comportant que quelques centaines d'atomes. La mécanique moléculaire s'appuie sur 3 principes qui simplifient l'approche physique :
Les atomes qui constituent les molécules sont représentés, dans certains modèles, par des boules reliées par des bâtonnets (les liaisons) :
Les interactions physiques entre atomes sont décrites par l'équation de l'énergie potentielle. Le principe clé est que la conformation spatiale optimale est caractérisée par l'énergie la plus basse. Il faut donc minimiser l'énergie par diverses méthodes (plus grande pente, Newton-Raphson, recuit simulé, gradients conjugués, ...). Si le système d'équations utilisé le permet, la mécanique moléculaire permet de décrire certaines propriétés des molécules : arrangement géométrique des atomes, stabilité des conformères, calcul des propriétés des molécules (moment dipolaire, polarisabilité, vibration, ...), forces qui s'exercent entre les molécules, rôle du solvant, éventuellement la réactivité chimique, ... |
a. Les catégories de méthodes de mécanique moléculaire La figure ci-dessous décrit les gammes d'application des méthodes de modélisation moléculaire à différentes résolutions (échelles approximatives de temps et de longueurs de système) : méthodes quantique ("quantum"), tout-atome ("all-atom"), à grain grossier ("coarse-grained") et méso-échelle ("mesoscale"). Les gammes d'applications peuvent être étendues en fusionnant des outils de résolutions différentes.
Source : Kmiecik et al. (2016) Les catégories de méthodes sont donc liées au nombre d'atomes des molécules dont on veut calculer l'énergie : a. Petites molécules (environ < 300 atomes) : méthodes quantiques - les interactions des noyaux et des électrons sont décrites explicitement. b. Méthodes dites tout atome (systèmes jusqu'à 100.000 atomes) : les atomes sont assimilés à des sphères et les interactions sont représentées par des oscillateurs autour d'une position d'équilibre. Ces positions d'équilibres constituent ce qu'on appelle le champ de force qui sert de référentiel. c. Méthode de simulation à granularité grossière ("Coarse - Grained" - CG) : elles permettent d'explorer des échelles de temps et d'espace inaccessibles aux modèles traditionnels de résolution atomique. L'eau étant le solvant universel de tous les systèmes biologiques, son traitement moléculaire est crucial dans les études de simulation. L'une des principales simplifications des modèles CG est donc la représentation du solvant : celle-ci est soit implicite, soit modélisée explicitement comme une particule de van der Waals. Figure ci-dessous : comparaison des caractéristiques de 2 simulations d'ordres de grandeur très différents. Sont indiqués : l'entité biologique étudiée; le type de simulation; le nombre d'atomes - particules (y compris l'eau) inclus dans la simulation; la dimension approximative linéaire de la boîte de simulation; la durée du cycle de production de la simulation; la taille du fichier résultant de la trajectoire.
Source : Chavent et al. (2016) Figure ci-dessous : Représentation tout atome d'un tripeptide et modèles à grains grossiers ("coarse-grained models") correspondants : mode de représentation centroïde de la méthode Rosetta, modèle de Levitt et Warshel et modèle SICHO. Les atomes de la chaîne latérale sont en orange et les pseudo-liaisons de longueur fluctuante sont représentées sous forme de ressorts.
Source : Kmiecik et al. (2016) Le mode de représentation centroïde est un mode de représentation réduit, qui simplifie la représentation du système et permet un échantillonnage et une notation plus rapides. Pour les protéines, chaque résidu d'acide aminé est représenté par 5 atomes du squelette carboné (N, Cα, C, O et H lié à N) et 1 pseudo-atome appelé centroïde (CEN) qui représente la chaîne latérale dont le rayon et les propriétés (polarité, charge, …) sont déterminés par l'identité du résidu. |
b. Fonction d'interaction et équations de mouvement
|
c. Algorithme de résolution des équations du mouvement Les trajectoires de l'espace des phases, caractérisées par une petite différence de conditions initiales, divergent de manière exponentielle au bout d'un certain temps : il n'existe donc pas d'algorithme d'intégration des équations du mouvement qui permette d'obtenir une solution exacte. Une solution satisfaisante est en revanche obtenue avec des algorithmes qui calculent de bonnes approximations des équations différentielles sur des temps courts. L'algorithme d'intégration de Loup Verlet (1967) est fréquemment utilisé car il fournit des solutions stables pour des temps plus longs. Cet algorithme réduit les erreurs : la position pour un pas de temps donné est calculée à partir de la position précédente et de la position actuelle sans utiliser la vitesse.
L'accélération ai(t + Δt) ne dépend que de la position ri(t + Δt) et non de la vitesse vi(t + Δt).
Principales sources :
|
d. Divers paramètres de construction du système étudié Conditions aux limites périodiques ("Periodic Boundary Conditions", PBC) Malgré la puissance des ordinateurs actuels, la taille des systèmes analysables sont microscopiques. Sans précautions particulières, seules des "gouttelettes infinitésimales" seraient simulées, or les propriétés de tels objets sont dominées par les effets de surface.
Ces boîtes environnantes sont dénommées boîtes d'image par certains logiciel comme CHARMM. Il s'agit souvent de boîte de simulation cubique (ou n'importe quel groupe d'espace cristallographique valide). Le rôle de ces boîtes environnantes est de remplacer les particules qui quittent la boîte de simulation centrale. En effet, les positions des particules sont recalculées en permanence par un calcul de minimisation ou d'une simulation de dynamique moléculaire.
A : 1 molécule d'adénine dans une boîte périodique avec 511 molécules d'eau / B : simulation d'un système périodique Sources : Molecular Modeling Basics & texample.net Traitement du solvant biologique : l'eau L'eau dans la cellule joue un rôle fondamental dans l'acquisition de la structure des protéines (des macromolécules biologiques de manière générale) et des fonctions qui en découlent (reconnaissance protéines - ligands, catalyse enzymatique, interactions entre protéines, ... ). Le solvant est traité de manière explicite : la molécule de protéine est placée dans une "boîte de solvant" répliquée en 3D (voir ci-dessus) ce qui simule l'environnement aqueux cellulaire. Lorsqu'une molécule quitte la boite centrale, ses images dans les cellules avoisinantes la remplacent. Cela évite les effets de bords et la dispersion des molécules d'eau : le nombre de particules est constant dans la maille cristallographique unitaire. Sur le plan théorique, voir la sommation d'Ewald ("Particle Mesh Ewald", PME), Erwin Madelung (1918) et Paul Ewald (1921) : calcul de l'énergie potentielle d'ions dans les cristaux. |
|
2. Le champ de force associé aux atomes d'une protéine Voir un cours : "La mécanique moléculaire" (Unisciel). Les atomes sont donc traités comme des boules de différentes tailles reliées entre elles par des ressorts (les liaisons) de différentes longueurs. Un champ de force est associé à chaque atome dans la protéine. Le schéma ci-dessous représente les cinq types de potentiels élémentaires d'un champ de force "simple" :
Source : Scistyle & Folding@home
|
| a. Exemples de formulation des termes d'un champ de force |
L'énergie totale Etotale (appelée aussi énergie potentielle) d'une protéine est donnée par l'équation suivante : Etotale = Eatomes liés covalemment + Eatomes non liés covalemment = [Estretch + Ebend + Etorsion + Eimproper] + [EVdW + Eelec] (en N.m ou J) |
||
| Estretch : l'énergie d'élongation (ou de tension - "bond stretching") d'une liaison par rapport à sa distance d'équilibre est une fonction quadratique. |
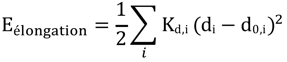 |
|
| Ebend : l'énergie de déformation angulaire ou de courbure des angles ("angle bending") par rapport aux angles de valence standard est une fonction quadratique. | 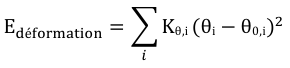 |
|
Etorsion : énergie de torsion dihédrale ("bond rotation - dihedral torsion")
|
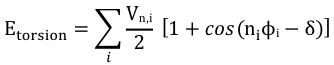 |
Un angle dièdre est l'angle entre les plans formés par 2 séries de 3 atomes, ayant 2 atomes en commun.
|
| Eimproper : énergie de torsion dihédrale impropre | Eimproper = kimproper (ω - ω0)2 | Un type d'angles dièdres (appelé dièdre impropre, "improper dihedral") est utilisé pour forcer les atomes à rester dans un plan ou pour empêcher une configuration de chiralité opposée. |
Schéma ci-contre : interactions entre 2 atomes non liés covalemment. L'énergie totale de rotation autour d'une liaison est la somme :
|
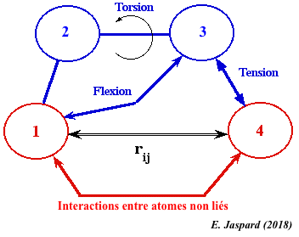 |
Cette interaction est responsable de l'encombrement stérique qui joue un rôle important dans la géométrie des protéines. Cette interaction résulte de l'attraction de van der Waal et de [l'attraction/répulsion] électrostatique qui s'exercent sur ces deux atomes. |
EVdW : énergie des interactions de Van der Waals entre atomes non liés covalemment ("non-bonded interactions"). Elle est exprimée en général sous la forme d'un potentiel de John Lennard-Jones (dispersion et de répulsion) ou d'un potentiel de Buckingham). |
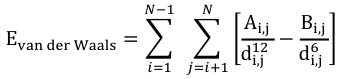 |
|
Eelec : énergie des interactions électrostatiques entre atomes non liés covalemment. Elle est exprimée en utilisant un potentiel Coulombien. Ce terme augmente avec la polarité des liaisons chimiques et peut être particulièrement important, par exemple dans le cas de molécules qui contiennent des hétéroatomes. |
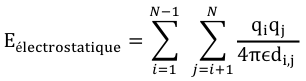 |
|
Exemple d'une autre formulation de Eelec : potentiel de Coulomb avec une longueur de criblage de Debye (λD) appliquée à tous les résidus avec des charges non nulles qi. |
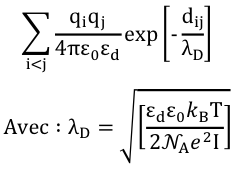 |
|
Le nombre de termes, leur complexité, leur sophistication dépendent des auteurs qui développent un champ de force. Les champs de force les plus récents sont plus sophistiqués et incluent des termes mixtes qui tiennent compte des interdépendances des différents types d'interactions. |
||
b. Exemples de champs de force en mécanique et en dynamique moléculaires Selon la méthode de calcul utilisée pour le calcul de l'énergie, les structures moléculaires modélisées et leurs propriétés seront ou non exactes. Le choix du champ de force est donc à faire en se basant sur les résultats déjà obtenus dans la littérature concernant leurs applications aux systèmes moléculaires.
Les champs de force sont constamment améliorés et sophistiqués du fait de l'essor des études des macromolécules biologiques (mise au point de médicaments et "docking") par chimie informatique, de l'accroissement des capacités de calculs des ordinateurs (dynamique moléculaire) et de l'évolution des langages de programmation.
|
| Un fichier PSF ("Protein Structure File") contient les informations (spécifiques d'une molécule) nécessaires pour lui appliquer un champ de force. | |
|
Par exemple, le champ de force CHARMM contient, entre autres, un fichier de topologie qui génère le fichier PSF. Exemple ci-dessous : extrait du fichier PSF pour l'ubiquitine (qui commence par le titre et les données des atomes) : PSF CMAP 6 !NTITLE
REMARKS original generated structure x-plor psf file
REMARKS 2 patches were applied to the molecule.
REMARKS topology top_all27_prot_lipid.inp
REMARKS segment U { first NTER; last CTER; auto angles dihedrals }
REMARKS defaultpatch NTER U:1
REMARKS defaultpatch CTER U:76
1231 !NATOM 1 U 1 MET N NH3 -0.300000 14.0070 0 2 U 1 MET HT1 HC 0.330000 1.0080 0 3 U 1 MET HT2 HC 0.330000 1.0080 0 4 U 1 MET HT3 HC 0.330000 1.0080 0 |
Le champ de force CHARMM contient également un fichier de paramètres qui contient les valeurs numériques spécifiques pour la fonction potentielle générique CHARMM :
|
| Voir une liste de programmes sur le site de la PDB. | |
c. Minimisation de la fonction d'énergie de la structure des protéines La conformation qu'adopte une protéine est d'autant plus stable que son énergie est faible. La mécanique moléculaire a donc pour but de calculer le minimum de la fonction d'énergie Etotale décrite ci-dessus.
Les paysages énergétiques conformationnels des protéines ("protein conformational energy landscapes") sont des surfaces complexes de grande dimension avec de nombreux minima locaux (figure ci-dessous).
Sources : (à gauche) "Single Molecule Protein Dynamics" - (à droite) Kuhlman & Bradley (2019)
Certains algorithmes d'optimisation sont basés sur le calcul du gradient : les dérivées de la fonction d'énergie par rapport aux degrés de liberté flexibles (par exemple les coordonnées atomiques ou les angles de torsion) sont calculées afin de cheminer dans la direction où l'énergie diminue le plus rapidement. Les méthodes basées sur les gradients sont efficaces pour trouver un minimum local mais le sont peu pour trouver le minimum global. Si on considère le vecteur V qui décrit les coordonnées des atomes, l'optimisation de la géométrie de la molécule consiste à trouver la valeur de V pour laquelle l'énergie en fonction des positions, E(V), est minimale : la dérivée de l'énergie par rapport à la position des atomes, ∂E/∂V = 0. La logique algorithmique est schématiquement la suivante :
|
| Exemples d'algorithmes et de méthodes de minimisation | |
| Algorithme du gradient (ou de plus profonde descente, "steepest descent") | Il suit le gradient de la fonction d'énergie en calculant la pente. Il est efficace au début de la recherche mais il converge mal. Il ne peut pas "franchir" les barrières d'énergie. |
| Méthode du gradient conjugué ("conjugate gradient") | Elle tient compte de valeurs du gradient calculées aux étapes précédentes : elle ajoute un vecteur orthogonal à la direction en cours de l'optimisation, puis les déplace dans une direction presque perpendiculaire à ce vecteur. Avec des conditions initiales bien choisies, elle aboutit à une estimation proche de la solution exacte en quelques itérations. |
| Méthode de Newton-Raphson | Elle utilise la dérivée seconde : le minimum de la fonction est approché par le développement de Taylor au second degré. Elle requière peu d'étapes mais nécessite plus de ressources (calcul de l'inverse de la matrice hessienne). Voir scipy.optimize.newton (Python - scipy). |
| Les algorithmes génétiques ("genetic algorithms") | Il s'agit de métaheuristiques inspirées du processus de sélection naturelle : initialisation de la population / sélection / crossover. Ils sont efficaces pour trouver un minimum global à partir d'une configuration initiale aléatoire. Exemples : "Birmingham parallel genetic algorithm" (nanoparticules, super calculateur). |
| Les méthodes Monte Carlo | I-TASSER ("Iterative Threading ASSEmbly Refinement", méthode et serveur Web) : méthodes d'assemblage de structures de fragments à l'aide d'une simulation Monte Carlo d'échange de répliques. C'est l'une des méthodes de prédiction de la structure des protéines les plus performantes dans les expériences CASP. PELE ("Protein Energy Landscape Exploration"). |
| scipy.optimize.basinhopping (Python - scipy) | Trouver le minimum global d'une fonction en utilisant l'algorithme de saut de bassin ("basin-hopping algorithm"). |
| Exemples de serveurs web pour l'affinement de structures (méthodes testées via l'expérience CASP) | |
| Mobyle | a portal for bioinformatics analyses (RPBS Web Portal, Université Paris Diderot) |
| PREFMD | Protein structure REFinement via Molecular Dynamics |
| locPREFMD | local Protein structure REFinement via Molecular Dynamics |
| GalaxyWEB | web server for protein structure prediction, refinement, and related methods |
| ModRefiner | algorithm for atomic-level, high-resolution protein structure refinement |
| 3DRefine | protein structure refinement server |
| AIR | Artificial Intelligence-based protein structure Refinement method |
3. Modélisation de structures de protéines par homologie ("Homology modeling") Les algorithmes de comparaison de structures 3D de deux protéines peuvent être classés en plusieurs catégories :
|
a. Démarche de la modélisation par homologie La structure inconnue (que l'on veut modéliser) est appelée cible ("target") et la structure connue est appelée modèle ("template").
Recherche (reconnaissance) d'un modèle et alignement initial ("template recognition and initial alignment") La séquence de la protéine de structure inconnue (cible) est comparée aux séquences des protéines dont les structures sont connues et stockées dans la banque de données de structures de protéines (Exemple : "Protein Data Bank" - PDB). Cette recherche de modèle dans la base de données s'effectue avec un programme tel que PSI-BLAST (utilisation d'un profil plus spécifique de la protéine cible) : elle renvoie la liste des protéines de structures connues (les modèles potentiels) qui correspondent à la séquence cible. La recherche d'un modèle correct est plus difficile quand on a une protéine cible qui contient de multiples domaines. Si BLAST ne trouve pas de modèle, une technique plus sophistiquée est nécessaire pour identifier la structure d'une molécule : le "protein threading", la modélisation "ab initio". Correction des alignements multiples Les alignements multiples doivent être corrigés (optimisés) avec des programmes tels que T-Coffee ou Muscle et aussi par une inspection visuelle ("à la main"). Il est nécessaire d'identifier les résidus d'acides aminés qui doivent être conservés. Par exemple : un changement Ala (hydrophobe) -> Glu (chargé) est possible, mais il est peu probable qu'il se produise dans une région hydrophobe, donc ces 2 résidus ne doivent pas être alignés. La structure du modèle indique les résidus potentiellement situés à l'intérieur, moins susceptibles de substitution que ceux situés à la surface de la protéine. Par ailleurs, les alignements de séquences introduisent des "gaps" (insertion - délétion de résidus d'acides aminés). Les insertions - délétions sont davantage compatibles avec la conservation de la structure si elles ont lieu dans des régions divergentes (par exemple, en dehors des régions qui adoptent une structure secondaire). Les alignements multiples corrigés ont pour but de de mettre en évidence ces régions. Les gaps doivent être aussi peu nombreux et contigus que possible. Enfin des acides aminés critiques tels que ceux qui constituent le site actif d'une enzyme doivent être hautement conservés. Modélisation des boucles S'il y a un/des gap(s) dans la séquence cible, on supprime le/les résidu(s) correspondant(s) dans le modèle. S'il y a une insertion dans la cible, c'est le modèle qui contient un gap : en d'autres termes, il n'y a pas de coordonnées tridimensionnelles pour ce résidu additionnel dans le modèle. En conséquence, le squelette carboné du modèle doit être "coupé" pour insérer ce résidu. Des modifications de cette ampleur ne sont pas modélisables dans des éléments de structures secondaires : ils doivent être placés dans des boucles. Les boucles à la surface des structures de protéines sont flexibles donc difficiles à prédire. Une méthode consiste donc à inclure des résidus d'acides aminés avant et après l'insertion (ce sont des résidus dits d'ancrage - "anchor-residues") puis de rechercher dans la base de données PDB les boucles qui possèdent les mêmes résidus d'ancrage : la boucle la plus similaire est copiée dans le modèle.
|
b. Validation de la structure de la protéine cible construite à partir du modèle Exemples de caractéristiques structurales qu'il est indispensable de valider pour proposer une structure qui représente de manière fiable la protéine que l'on veut modéliser. Un angle dièdre est l'angle formé entre 2 plans en intersection. Dans la structure des protéines, c'est l'angle entre les plans formés par 2 séries de 3 atomes, ayant 2 atomes en commun. Dans une chaîne polypeptidique, on définit 3 angles dièdres qui sont reportés dans les diagrammes de Ramachandran :
La planarité de la liaison peptidique limite généralement ω à 0° (conformation cis, rare - principalement observé dans les liaisons peptidiques acide aminé-Pro) ou à 180° (conformation trans, la plus fréquente) . La distance entre les atomes Cα des isomères cis et trans est respectivement d'environ 2.9 Å et 3.8 Å.
Source : Expasy - SwissModel
|
| Portée de la validation | |||
| tests géometriques | faible | facteur de température | faible |
| angle ω | faible | résolution | modérée |
| combinaisons Φ, Ψ | très forte | facteur R | faible |
| carbones alpha ("CA-only tests") | forte | facteur Rfree | très forte |
| analyse DACA | très forte | facteur Rfree - R | forte |
| symétrie non-cristallographique | modérée | estimées des coordonnées | modérée |
Voir un cours très complet sur la validation des structures modélisées. Voir : CAMEO ("Continuous Automated Model EvaluatiOn"). Représentation d'un diagramme de Ramachandran (script Python). |
|||
4. Les scores de distances inter-atomiques entre des structures comparées La modélisation par homologie de structures nécessite de superposer les structures des protéines qui sont comparées pour établir la correspondance spatiale entre les acides aminés équivalents dans ces structures. Le score RMSD ("Root Mean Square Deviation") et le score RMSD local Pour mesurer les distances inter-atomiques on utilise fréquemment une grandeur appelée écart quadratique moyen (RMSD, en Å) entre les coordonnées spatiales des atomes des acides aminés appariés. Par exemple, si on considère n atomes de 2 structures, on compare les coordonnées (xi, yi, zi) d'un atome i de l'une de ces structures aux coordonnées (x'i, y'i, z'i) d'un atome i apparié de l'autre structure : on superpose ainsi les structures en minimisant la valeur de RMSD.
Limites du score RMSD
Pour effectuer un choix pertinent des acides aminés à comparer, on calcule un RMSD local avec les carbones α des acides aminés inclus dans une fenêtre de longueur L+1 :
Des équations ont été proposées pour établir un lien entre la déviation du RMSD des repliements et le degré d'homologie des séquences. Le score GDT ("Global Distance Test") C'est aussi une mesure de la similarité entre 2 structures protéiques qui ont des structures tertiaires différentes. Ce score est calculé sur la base du plus grand ensemble de carbone α des résidus d'acides aminés de la structure de la protéine cible dont la position dans l'espace correspond (selon un seuil donné : 1 Å, 2 Å, 4 Å et 8 Å) à celles des résidus d'acides aminés de la structure de la protéine modèle. Les scores GDT sont les principaux critères d'évaluation des résultats de prédiction issus de l'expérience CASP ("Critical Assessment of Structure Prediction"). CASP est une expérience à grande échelle de la communauté scientifique qui travaille sur la prédiction de structure. CASP évalue et améliore les différentes techniques de modélisation de structures de protéines. Le score TM ("Template Modeling score") C'est également une mesure de la similarité entre 2 structures protéiques qui ont des structures tertiaires différentes. Le score TM est une mesure plus précise de la qualité des structures protéiques que le score RMSD et le score GDT. Dans le calcul du score TM, les distances faibles ont un poids plus élevé que les distances fortes : ce score est donc insensible aux erreurs de modélisation locales.
Exemples de comparaisons et de scores de comparaisons Figure ci-dessous : superpositions des structures de 2 protéines avec différents algorithmes (CE - "Combinatorial Extension of the optimal path", SAL, DALI et TM-align).
L est le nombre de résidus d'acides aminés alignés. Les scores RMSD et TM sont indiqués.
Source : Zhang & Skolnick (2005) Le score lDDT ("Local Distance Difference Test") Il est calculé sur toutes les paires d'atomes dans la structure de référence à une distance inférieure à un seuil prédéfini (appelé rayon d'inclusion), et n'appartenant pas au même résidu d'acide aminé. Ces paires d'atomes définissent un ensemble de distances locales L :
Pour un seuil donné, la fraction des distances conservées est calculée. Le score IDDT est la moyenne de 4 fractions calculées en utilisant des seuils identiques à ceux utilisés pour calculer le score GDT (voir ci-dessus). Divers Voir un très grand nombre de programmes de superposition de structures. |
5. Exemples de programmes de modélisation et de visualisation de structures de protéines PyMOL est un programme de modélisation par homologie et de visualisation de structures de molécules (écrit en partie en Python). Il existe des versions pour plusieurs environnements (MacOS, Windows, Linux). Plugin PyMod pour PyMOL : recherches de similarité de séquence, alignements séquence à structure multiple, modélisation par homologie. C'est une interface simple et intuitive entre PyMOL et plusieurs outils bioinformatiques (exemples : PSI-BLAST, Clustal, Muscle, PSI-PRED, MODELLER, ...). Figure ci-dessous : procédure de "PyMod" qui intègre divers types de données et permet divers types d'analyses.
Source : Bramucci et al. (2012)
Chaque "bloc de procédure" est indépendant des autres : on peut donc, par exemple, effectuer un alignement de séquences multiples sans recherche préalable dans une base de données. Voir la syntaxe de la commande "align" de PyMOL. |
|
Logiciels libres de visualisation de structures de molécules. JSmol ("Jmol JavaScript Object")
Jmol est l'applet écrite en Java, précurseur de JSmol. Il existe des versions pour plusieurs environnements (MacOS, Windows, Linux). |
|
7 atomes d'oxygène constitue le réseau de coordination du calcium :
|
|
C'est un logiciel de modélisation de structures de protéines par homologie.
La recherche de séquences similaires dont les structures sont connues est effectuée avec la commande "profile. build ()" (contenue dans le script "build_profile.py") du programme MODELLER. Le script "build_profile. py" effectue les opérations suivantes : 1. Il initialise l'environnement de la modélisation en créant un objet "environ" (appelé "env"). Presque tous les scripts MODELLER nécessitent cette étape, car ce nouvel objet est nécessaire pour construire la plupart des autres objets utiles à la modélisation. 2. Il crée un objet "sequence_db" (appelé "sdb") utilisé pour contenir de grandes bases de données de séquences de protéines. 3. Il lit, dans la base de données "sdb", un fichier (au format texte) contenant des séquences non redondantes de la PDB. Les séquences sont aussi dans le fichier "pdb_95.pir" au format PIR. Chaque séquence de ce fichier est représentative d'un groupe de séquences de la PDB qui ont 95% ou plus d'identité de séquence et qui ont moins de 30 résidus ou une différence de longueur de séquence inférieure à 30%. 4a. Il écrit un fichier au format binaire contenant toutes les séquences lues à l'étape précédente. 4b. Il relit le fichier au format binaire pour une exécution plus rapide du script.
5a. Il crée un objet "alignment" ("aln"). 5b. Il lit la séquence cible TvLDH (dans l'exemple choisi) à partir du fichier "TvLDH.ali". 5c. Il convertit la séquence cible lue en un objet "profil " (appelé "prf"). Les profils contiennent des informations similaires à celles des alignements, mais ils sont plus compacts, plus complets et plus performants pour une recherche dans la base de données de séquences. 6. L'instruction "prf.build()" effectue la recherche dans "sdb" avec le profil "prf". Les correspondances qui sont trouvées sont ajoutées au profil. 7. L'instruction "prf.write()" écrit le nouveau profil contenant la séquence cible et ses homologues dans le fichier (au format texte) de sortie spécifié (le fichier "build_profile.prf"). 8. Conversion du nouveau profil en un nouvel alignement. 9. L'instruction "aln.write()" écrit le nouvel alignement contenant la séquence cible et ses homologues dans le fichier (au format PIR) de sortie spécifié (le fichier "build_profile.ali"). Récupérer le script "build_profile.py". Exécution du script Si le fichier est enregistré avec le nom "toto.py" et si la version de MODELLER est 9.19 (juillet 2017), la commande pour exécuter ce script est "mod9.19 toto.py".
Voir un descriptif très précis de toutes les étapes de MODELLER. |
d. MODELLER : détail de la syntaxe de la commande profile.build() Cette commande analyse (de manière itérative) une base de données contenant un très grand nombre de séquences protéiques dans le but de créer un profil pour la séquence (ou l'alignement) que l'on veut modéliser. Cette commande calcule le score d'un alignement local (méthode de Smith-Waterman) entre la séquence à modéliser et chacune des séquences de la base de données. build( Les alignements avec des E-values inférieures à la valeur du paramètre "max_aln_evalue" sont ajoutés à l'alignement en cours. Une matrice PSSM ("Position Specific Scoring Matrix") est générée à partir de l'alignement en cours : cette matrice est utilisée pour rechercher dans la base de données de séquences choisies. Cette procédure itérative est répétée :
Remarque : la recherche d'un repliement nécessite un drapeau "gaps_in_target=True". |
e. Autres logiciels de modèlisation structurale par homologie
|
|
Le terme "protein threading" n'est pas facile à traduire, car "threading" a pour signification "filetage, enfiler une aiguille". On peut donc traduire cette expression par :
C'est donc une méthode de modélisation de la structure des protéines utilisée pour une protéine :
En conséquence, bien que comparable, la démarche "protein threading" se distingue de la modélisation par homologie de structure :
Etapes du "protein threading"
Le serveur de prédiction de structures de protéines et le programme HHpred
HHpred :
|
7. Démarche "de novo protein design" : exemple de la protéine "artificielle" TOP7 C'est une protéine "artificielle" de 93 acides aminés issue de simulations / calculs de prédiction ("de novo protein design") effectués par B. Kuhlman et G. Dantas (Université de Caroline du Nord) . Ces chercheurs ont utilisé comme point de départ un repliement encore jamais mis en évidence dans la nature. Les séquences ont été générées avec le programme "Rosetta design Monte Carlo search protocol and energy function" : un potentiel de Lennard-Jones 12-6; un terme pour les liaisons hydrogène dépendant de l'orientation; un modèle de solvatation implicite. Tous les acides aminés (excepté la cystéine) ont été autorisés pour 71 des 93 positions (≈ 110 rotamères par position) et les 22 positions restantes (surface des feuillets) ont été restreintes à des acides aminés polaires (≈ 75 rotamères par position). L'espace de recherche était de 11071 × 7522, soit ≈ 10186 rotamères. Les conformations du squelette carboné ont été générées sans contrainte pour optimiser la compacité des chaînes latérales : en conséquence, les séquences de plus basse énergie avaient une énergie très supérieure à celle de protéines natives de même taille.
La comparaison de la structure modèle conçue par calcul et de la structure cristalline est saisissante :
|
|
Visualisation de TOP7 à une résolution de 2,5 Å Le chargement de la structure peut prendre du temps. Code PDB : 1QYS |
Ci-dessous, aperçu de quelques méthodes de modélisation et de cadres de conception de macromolécules dans l'environnement Rosetta.
Source : Leman et al. (2020) |
| 9. Liens Internet et références bibliographiques |
|
"Introduction à la structure des protéines" - C. Branden & J. Tooze (1996) - ed. De Boeck Université Anfinsen et al. (1961) Proc. Natl. Acad. Sci. USA 47, 1309 - 1314 Levinthal C. (1968) "Are there pathways for protein folding ?" J. Chem. Phys. 65, 44 - 45 Baaden M. (2003) "Dynamique Moléculaire in silico : Fondements théoriques et liste détaillée de références bibliographiques" Ecole thématique du CNRS Thèse Leroux V. (2006) "Modélisation d'inhibiteurs du domaine SH2 de la protéine Grb2 par dynamique moléculaire, docking et criblage virtuel" |
|
Voir une liste quasi exhaustive des programmes de mécanique et modélisation moléculaires. The Nobel Prize in Chemistry 2013 was awarded jointly to Martin Karplus, Michael Levitt and Arieh Warshel "for the development of multiscale models for complex chemical systems". |
|
"RosettaAThome": détermination de structures tridimensionnelles avec temps de calcul partagé FragBuilder: bibliothèque pour des calculs de chimie quantique avec des peptides modèles ProDy : ensemble de scripts ("free and open-source Python package") pour l'étude de la dynamique structurale des protéines "ASTRO-FOLD : Protein Structure Prediction from First Principles" SWISS-MODEL Repository (SMR) : base de données de modèles de structures protéiques 3D annotées |
|
|
Kuhlman et al. (2003) "Design of a Novel Globular Protein Fold with Atomic-Level Accuracy" Science 302, 1364 - 1368 Zhang & Skolnick (2004) "Scoring function for automated assessment of protein structure template quality" Proteins 57, 702 - 710 Zhang & Skolnick (2005) "TM-align: a protein structure alignment algorithm based on the TM-score" Nucleic Acids Res. 33, 2302 - 2309 Eswar et al. (2006) "Comparative Protein Structure Modeling with MODELLER" Current Protocols in Bioinformatics, John Wiley & Sons, Inc., Supp. 15, 5.6.1-5.6.30 Marrink et al. (2007) "The MARTINI force field: coarse grained model for biomolecular simulations" J. Phys. Chem. B. 111, 7812 - 7824 |
Article |
|
Petridis & Smith (2009) "A molecular mechanics force field for lignin" J. Comput. Chem. 30, 457 - 467 Jamros et al. (2010) "Proteins at work: a combined small angle X-RAY scattering and theoretical determination of the multiple structures involved on the protein kinase functional landscape" J. Biol. Chem. 285, 36121 - 36128 Regad et al. (2011) "Dissecting protein loops with a statistical scalpel suggests a functional implication of some structural motifs" BMC Bioinformatics 12, 247 Mariani et al. (2013) "lDDT: a local superposition-free score for comparing protein structures and models using distance difference tests" Bioinformatics 29, 2722 - 2728 Ingolfsson et al. (2014) "The power of coarse graining in biomolecular simulations" Wiley Interdiscip. Rev. Comput. Mol. Sci. 4, 225 - 248 |
|
Webb & Sali (2016) "Comparative protein structure modeling using MODELLER" Curr. Protoc. Bioinformatics Chapter 5, unit 5.6 Kmiecik et al. (2016) "Coarse-grained protein models and their applications" Chem. Rev. 116, 7898 - 7936 Chavent et al. (2016) "Molecular dynamics simulations of membrane proteins and their interactions: from nanoscale to mesoscale" Curr. Opin. Struct. Biol. 40, 8 - 16 Lyubartseva & Rabinovich (2016) "Force field development for lipid membrane simulations" Biochim. Biophys. Acta - Biomembranes 1858, 2483 - 2497 |
|
|
Janson et al. (2017) "PyMod 2.0: improvements in protein sequence-structure analysis and homology modeling within PyMOL" Bioinformatics 33, 444 - 446 Bienert et al. (2017) "The SWISS-MODEL repository-new features and functionality" Nucleic Acids Res. 45, D313 - D319 Borgia et al. (2018) "Extreme disorder in an ultrahigh-affinity protein complex" Nature 555, 61 - 66 |
|
|
Kuhlman & Bradley (2019) "Advances in protein structure prediction and design" Nat. Rev. Mol. Cell Biol. 20, 681 - 697 Wang et al. (2020) "Artificial intelligence-based multi-objective optimization protocol for protein structure refinement" Bioinformatics 36, 437 - 448 Leman et al. (2020) "Macromolecular modeling and design in Rosetta: recent methods and frameworks" Nat. Methods 17, 665 - 680 Rahman et al. (2020) "Comparison and Evaluation of Force Fields for Intrinsically Disordered Proteins" J. Chem. Inf. Model. 60, 4912 - 4923 |
|